1. SEGUN EL CUENTO DEL MAGO DE OZ NUNCA HAY DOS DIAS BUENOS EN SUCESION O SEGUIDOS, DESPUES DE 1 DIA CON BUEN TIEMPO LE SIGUE CON IGUAL PROBABILIDAD LE SIGUE UN DIA CON LLUVIA O NIEVE, DEL MISMO MODO SI NIEVA O LLUEVE, EL DIA SIGUIENTE NEVARA O LLOVERA CON PROBABILIDAD 1/2, PERO SI CAMBIA EL TIEMPO SOLO LA MITAD DE LAS VECES SERA UN LINDO DIA.
Páginas
Buscar este blog
miércoles, 27 de noviembre de 2013
EJERCICIOS EN CLASE
1. SEGUN EL CUENTO DEL MAGO DE OZ NUNCA HAY DOS DIAS BUENOS EN SUCESION O SEGUIDOS, DESPUES DE 1 DIA CON BUEN TIEMPO LE SIGUE CON IGUAL PROBABILIDAD LE SIGUE UN DIA CON LLUVIA O NIEVE, DEL MISMO MODO SI NIEVA O LLUEVE, EL DIA SIGUIENTE NEVARA O LLOVERA CON PROBABILIDAD 1/2, PERO SI CAMBIA EL TIEMPO SOLO LA MITAD DE LAS VECES SERA UN LINDO DIA.
PROMODEL
ProModel es un simulador con animación para computadoras personales. Permite simular cualquier tipo de sistemas de manufactura, logística, manejo de materiales,etc. Puedes simular bandas de transporte, grúas viajeras, ensamble, corte, talleres, logística, etc.
ProModel es un paquete de simulación que no requiere programación, aunque sí lo permite. Corre en equipos 486 en adelante y utiliza la plataforma Windows®. Tiene la combinación perfecta entre facilidad de uso y flexibilidad para aplicaciones complejas.
Puedes simular Justo a Tiempo, Teoría de Restricciones, Sistemas de Empujar, Jalar, Logística, etc. Prácticamente, cualquier sistema pueder ser modelado.
Una vez hecho el modelo, éste puede ser optimizado para encontrar los valores óptimos de los parámetros claves del modelo. Algunos ejemplos incluyen determinar la mejor combinación de factores para maximizar producción minimizando costo, minimizar el número de camiones sin penzliar el servicio, etc.
El módulo de optimización nos ayuda a encontrar rápidamente la solución óptima, en lugar de solamente hacer prueba y error. ProModel cuenta con 2 optimizadores disponibles y permite de esta manera explotar los modelos de forma rápida y confiable.
Beneficios Clave
- Único software de simulación con Optimización plenamente intregrada
- Creación de modelos rápida, sencilla y flexible.
- Modelos optimizables.
- Elementos de Logística, Manejo de Materiales, y Operaciones incluídas. (Bandas de transporte, Grúas Viajeras, Operadores).
- Entrenamiento en Español.
- Resultados probados.
- Importación del Layout de Autocad, y cualquier herramienta de CAD / CAE / Diseño, así como de fotografías digitales.
- Soporte Técnico 24 horas al día, 365 días del Año.
- Integración a Excel, Lotus, Visual Basic y herramientas de Microsoft.
- Genera en automático las gráficas en 3 dimensiones para visualización en el espacio tridimensional
CADENAS DE MARKOV
CADENAS DE MARKOV
Un proceso o sucesión de eventos que se desarrolla en el
tiempo en el cual el resultado en cualquier etapa contiene algún elemento que
depende del azar se denomina proceso aleatorio o proceso estocástico. Por
ejemplo, la sucesión podría ser las condiciones del tiempo en Paraná en una
serie de días consecutivos: el tiempo cambia día a día de una manera que en
apariencia es algo aleatoria. O bien, la sucesión podría consistir en los precios
de las acciones que cotizan en la bolsa en donde otra vez interviene cierto
grado de aleatoriedad.
Un ejemplo simple de un proceso estocástico es una sucesión
de ensayos de Bernoulli, por ejemplo, una sucesión de lanzamientos de una moneda.
En este caso, el resultado en cualquier etapa es independiente de todos los
resultados previos (esta condición de independencia es parte de la definición
de los ensayos de Bernoulli). Sin embargo, en la mayoría de los procesos
estocásticos, cada resultado depende de lo que sucedió en etapas anteriores del
proceso. Por ejemplo, el tiempo en un día determinado no es aleatorio por
completo sino que es afectado en cierto grado por el tiempo de días previos. El
precio de una acción al cierre de cualquier día depende en cierta medida del comportamiento
de la bolsa en días previos.
El caso más simple de un proceso estocástico en que los
resultados dependen de otros, ocurre cuando el resultado en cada etapa sólo
depende del resultado de la etapa anterior y no de cualquiera de los resultados
previos. Tal proceso se denomina proceso de Markov o cadena de Markov (una
cadena de eventos, cada evento ligado al precedente)
Estas cadenas reciben su nombre del matemático ruso Andrei
Andreevitch Markov (1856-1922). Como mencionamos antes, estas cadenas tiene
memoria, recuerdan el último evento y eso condiciona las posibilidades de los
eventos futuros. Esto justamente las distingue de una serie de eventos
independientes como el hecho de tirar una moneda. Este tipo de proceso presenta
una forma de dependencia simple, pero muy útil en muchos modelos, entre las
variables aleatorias que forman un proceso estocástico. Se utilizan, por
ejemplo, para analizar patrones de compra de deudores morosos, para planear
necesidades de personal, para analizar el reemplazo de un equipo, entre otros.
Definición
Una cadena de Markov es una sucesión de ensayos similares u
observaciones en la cual cada ensayo tiene el mismo número finito de resultados
posibles y en donde la probabilidad de cada resultado para un ensayo dado
depende sólo del resultado del ensayo inmediatamente precedente y no de
cualquier resultado previo.
Propiedad de Markov: Dada una secuencia de variables
aleatorias ...... , , , X1 X2 X3, tales que el valor de Xn es el estado del
proceso en el tiempo n. Si la distribución de probabilidad condicional de Xn+1 en
estados pasados es una función de Xn por sí sola,
Entonces:
Donde xi es el estado del proceso en el instante i.
Esta identidad es la denominada propiedad de Markov: El
estado en t + 1 sólo depende del estado
en t y no de la evolución anterior del sistema.
viernes, 25 de octubre de 2013
NUMEROS ALEATORIOS
Números
aleatorios definición propiedades, generadores y tablas.
Los números aleatorios son numeros
que deben de cumplir los requisitos de espacio equiprobable, es decir, que todo
elemento tenga la misma probabilidad de ser elegido y que la elección de uno no
dependa de la elección del otro. Son generados por medio de una función
determinista (no aleatoria) y que aparentan ser aleatorios.
Generadores
de números aleatorios
Los métodos para generar números
aleatorios involucran algún proceso físico cuasialeatorio, que genera
sucesiones de números aleatorios de determinada longitud. El requisito general
para las sucesiones es la independencia estadística. Para esto, existen varios
métodos:
·
Métodos manuales: Dispositivos
mecánicos o electrónicos, lanzamientos de monedas o dados, empleo de barajas,
ruletas. Son menos prácticos pero simples, lentos, atractivos, pedagógico. Pero no
pueden reproducirse.
·
Tablas de bibliotecas: Generados por
los métodos anteriores. Están en tablas. Siempre pueden reproducirse, pero es
un sistema lento. Determinados problemas
requieren más números aleatorios que los
publicados.
·
Métodos de computación analógica: Dependen
de procesos físicos aleatorios, por ejemplo: el ruido térmico de un circuito
con semiconductores, que convertido en
un número binario, representa un valor numérico aleatorio. Se considera que
conducen a verdaderos números aleatorios.
·
Métodos de computación digital: Se han
sugerido tres métodos para producir números aleatorios cuando se usan
computadoras digitales; provisión externa, generación interna, relación de
recurrencia.
Existen en la actualidad técnicas
para generar con una computadora, variables aleatorias uniformemente distribuidas,
r (en donde r ≥ 0 y 1 ≥ r). Los
números generados por estas subrutinas de computadora se denominan números
pseudoaleatorios, porque se generan a partir de una fórmula totalmente
determinística mediante la computación. Sus propiedades estadísticas, coinciden
con las de los números generados a través de un dispositivo fortuito idealizado
que selecciona números de un intervalo unitario (0,1) de un modo independiente
en donde son igualmente probables todos los números.
A condición de que estos números
pseudo aleatorios puedan pasar el conjunto de pruebas estadísticas (las de
frecuencia, auto correlación, producto rezagado, corridas, de distancia y así
sucesivamente) implicadas por un dispositivo fortuito idealizado, tales números
pseudo aleatorios se pueden tratar corno si "en realidad lo fueran" a
pesar de que no lo son.
Comparativa
de métodos de generación
|
MÉTODOS
|
VENTAJAS
|
DESVENTAJAS
|
|
Manuales
|
Facil
generación
|
Lentos,
simples y poco prácticos
|
|
Tablas
|
Fácil
implementación
|
Lentos
y no reproducibles
|
|
Comp
Analógica
|
Rápidos
“ verdaderos”
|
No
reproducibles
|
|
Comp
Digital
|
Rápidos
|
No
son verdaderos
|
Requisitos
para un buen generador de números pseudo aleatorios con distribución uniforme:
·
La distribución de los números debe ser
uniforme en todo el intervalo [0,1].
·
Los
números deben ser independientes dentro de toda la serie generada.
·
El ciclo del generador debe ser lo
suficientemente grande.
·
La serie debe volverse a repetir.
·
Capaz de generar números pseudo
aleatorios a altas velocidades.
·
Requerir una mínima cantidad de la
capacidad de memoria de Computadora.
Ejemplos
de aplicación
·
Simulación: La reproducción de
fenómenos naturales necesita números aleatorios. En Física los ejemplos
clásicos: Física Estadística, Física de Partículas
·
Muestreo: Muchas veces es poco práctico
examinar todos los casos posibles. Un muestreo aleatorio puede revelar un
comportamiento típico.
·
Análisis Numérico: Técnicas numéricas
necesitan números aleatorios
·
Programación de ordenadores: Tests de
efectividad de algoritmos
·
Toma de decisiones: Se rumorea que
algunos ejecutivos tiran monedas al aire para tomar decisiones.
·
Estética: Un toque de aleatoriedad
puede resultar agradable
·
Juegos: De aquí proviene el propio
método para generación de números aleatorios
Fuente:
Sanchez,
Juan. Universidad Católica de Valparaíso.
http://www.material_simulacion.ucv.cl/en%20PDF/aleator11.pdf
Departamento
de Física Teórica. Universidad Complutense
http://teorica.fis.ucm.es/programas/MonteCarlo.pdf
Correa,
Gabriela. Universidad de Antioquia
http://docencia.udea.edu.co/ingenieria/isi-494/contenido/exposicion.html
Cómo generar números aleatorios con Excel
La función ALEATORIO (RAND en la versión inglesa) de Excel genera números aleatorios. Esta función no tiene argumentos y es recalculada nuevamente cada vez que se produce un cambio en la hoja, excepto que el modo de cálculo sea "manual".
Los números que produce ALEATORIO (RAND) van de del 0 al 1.
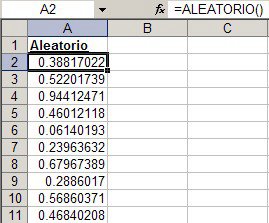
En esta hoja usamos la fórmula =ALEATORIO() en el rango A2:A11
Los números que produce ALEATORIO (RAND) van de del 0 al 1.
En esta hoja usamos la fórmula =ALEATORIO() en el rango A2:A11
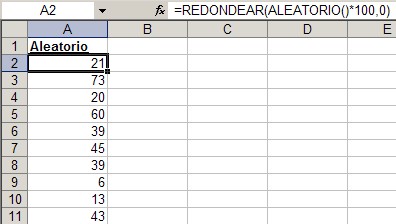
Si queremos producir una serie de números aleatorios enteros, debemos combinar la función ALEATORIO con la función REDONDEAR (ROUND), o con alguna otra función de este tipo como REDONDEAR.MAS o REDONDEAR.MENOS.
En esta hoja, usamos la fórmula combinada =REDONDEAR(ALEATORIO()*100,0) para producir números aleatorios entre 0 y 100
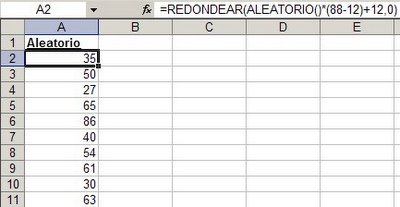
Si queremos producir números aleatorios que se encuentren en un rango entre dos números, digamos entre 12 y 88, podemos usar la fórmula
=REDONDEAR(ALEATORIO()*(88-12)+12,0)
Con esta técnica podemos generar, por ejemplo, números aleatorios para la lotería. Aquí, por ejemplo, el Loto sortea 6 números entre el 1 y el 36. El problema de esta fórmula es que puede generar números duplicados, como en este ejemplo
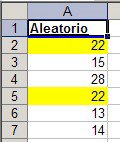
Supongo que hay más de una técnica para superar este problema. Mencionaré aquí dos de ellas.
La primera es, simplemente, recalcular la hoja (presionar F9) hasta lograr una serie sin números repetidos.
La otra consiste en condicionar la creación de los números aleatorios. Esta técnica consiste en generar una referencia circular intencional, para lo cual es necesario que la opción Iteración en Opciones/Cálculo esté activada (pueden bajar el archivo del ejemplo con las fórmulas
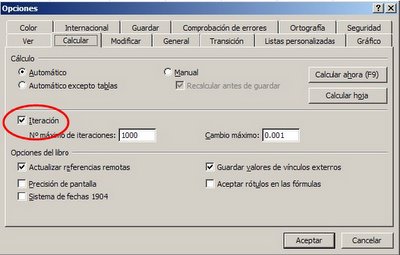
La fórmula que usamos en el rango A2:A11 es
=SI(SUMA($B$2:$B$11)<>10,REDONDEAR(ALEATORIO()*(36-1)+1,0),REDONDEAR(ALEATORIO()*(36-1)+1,0))
en el rango B2:B11 usamos la fórmula =CONTAR.SI($A$2:$A$11,A2). Esta fórmula controla si hay números duplicados. Si el resultado es 1, el número aparece una sola vez.
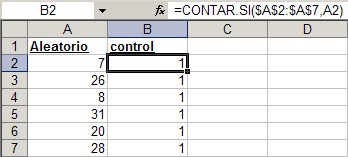
La fórmula en el rango A2:A11 controla si todos los resultados en el rango B2:B11 no suman 10, es decir que hay algún numero duplicado; en ese caso calcula un número aleatorio. Si la condición lógica no se cumple, vuelve a calcular. Como ven hay aquí una referencia circular. Como hemos activado la opción "Iteración", Excel intentará encontrar la serie de 10 números que cumplan con la condición. Si no la encuentra, deberemos pulsar nuevamente F9 (recalcular) hasta encontrar la solución.
Esta técnica fue sugerida por John Walkenbach en su libro "Microsoft Excel 2000 Formulas".
miércoles, 18 de septiembre de 2013
METODO DE MONTECARLO
El método
de Monte Carlo es un método no determinístico o
estadístico numérico, usado para aproximar expresiones matemáticas complejas
y costosas de evaluar con exactitud. El método se llamó así en referencia al Casino de Monte Carlo (Principado de Mónaco) por
ser “la capital del juego de azar”, al ser la ruleta un
generador simple de números aleatorios. El
nombre y el desarrollo sistemático de los métodos de Monte Carlo datan
aproximadamente de 1944 y se mejoraron enormemente con el desarrollo de la computadora.
El uso de
los métodos de Monte Carlo como herramienta de investigación, proviene del
trabajo realizado en el desarrollo de la bomba atómica durante la Segunda Guerra Mundial en
el Laboratorio Nacional de Los
Álamos en EE. UU. Este trabajo conllevaba la
simulación de problemas probabilísticos de hidrodinámica concernientes a la difusión de neutrones en el material de fisión. Esta difusión posee
un comportamiento eminentemente aleatorio. En la actualidad es parte fundamental de los algoritmos de Raytracing para la generación de imágenes 3D.
En la
primera etapa de estas investigaciones, John von Neumann y Stanislaw Ulam refinaron esta ruleta rusa y los métodos "de división" de
tareas. Sin embargo, el desarrollo sistemático de estas ideas tuvo que esperar
al trabajo de Harris y Herman Kahn en 1948.
Aproximadamente en el mismo año, Enrico Fermi, Nicholas Metropolis y
Ulam obtuvieron estimadores para los valores característicos de la ecuación de Schrödinger para
la captura de neutrones a nivel nuclear usando este método.
El método
de Monte Carlo proporciona soluciones aproximadas a una gran variedad de
problemas matemáticos posibilitando la realización de experimentos con
muestreos de números pseudoaleatorios en una computadora. El método es
aplicable a cualquier tipo de problema, ya sea estocástico o determinista. A diferencia
de los métodos numéricos que se basan en evaluaciones en N puntos en un espacio
M-dimensional para producir una solución aproximada, el método de Monte Carlo
tiene un error absoluto de la estimación que decrece como  en
virtud del teorema del límite central
en
virtud del teorema del límite central
ORIGENES DEL METODO
La invención del método de Monte Carlo se asigna a Stanislaw Ulam y a John von Neumann. Ulam ha explicado cómo se le ocurrió la idea mientras jugaba un solitario durante una enfermedad en 1946. Advirtió que resulta mucho más simple tener una idea del resultado general del solitario haciendo pruebas múltiples con las cartas y contando las proporciones de los resultados que computar todas las posibilidades de combinación formalmente. Se le ocurrió que esta misma observación debía aplicarse a su trabajo de Los Álamos sobre difusión de neutrones, para la cual resulta prácticamente imposible solucionar las ecuaciones íntegro-diferenciales que gobiernan la dispersión, la absorción y la fisión. “La idea consistía en probar con experimentos mentales las miles de posibilidades, y en cada etapa, determinar por casualidad, por un número aleatorio distribuido según las probabilidades, qué sucedería y totalizar todas las posibilidades y tener una idea de la conducta del proceso físico”.
Podían utilizarse máquinas de computación, que comenzaban a estar disponibles, para efectuar las pruebas numéricas y en efecto reemplazar el aparato experimental del físico. Durante una de las visitas de von Neumann a Los Álamos en 1946, Ulam le mencionó el método. Después de cierto escepticismo inicial, von Neumann se entusiasmó con la idea y pronto comenzó a desarrollar sus posibilidades en un procedimiento sistemático. Ulam expresó que Monte Carlo “comenzó a tener forma concreta y empezó a desarrollarse con todas sus fallas de teoría rudimentaria después de que se lo propuse a Johnny”.
A principios de 1947 Von Neumann envió una carta a Richtmyer a Los Álamos en la que expuso de modo influyente tal vez el primer informe por escrito del método de Monte Carlo. Su carta fue encuadernada junto con la respuesta de Richtmyer como un informe de Los Álamos y distribuida entre los miembros del laboratorio. Von Neumann sugería aplicar el método para rastrear la generación isótropa de neutrones desde una composición variable de material activo a lo largo del radio de una esfera. Sostenía que el problema era adecuado para el ENIAC y estimaba que llevaría 5 horas calcular la acción de 100 neutrones a través de un curso de 100 colisiones cada uno.
Ulam estaba particularmente interesado en el método Monte Carlo para evaluar integrales múltiples. Una de las primeras aplicaciones de este método a un problema determinista fue llevada a cabo en 1948 por Enrico Fermi, Ulam y von Neumann cuando consideraron los valores singulares de la ecuación de Schrödinger
lunes, 12 de agosto de 2013
SIMULACIÓN
La simulación es una indispensable metodología para la descripción y análisis de una amplia variedad de problemas reales. Usada apropiadamente, proporciona considerables beneficios según el contexto en la que se use: ahorro de tiempo; ahorro de recursos económicos; permite analizar la ocurrencia de ciertos fenómenos a través de la reconstrucción de escenas y un minucioso análisis, que no podría llevarse a cabo en una situación real; una vez desarrollado un modelo de simulación válido, se pueden explorar nuevas políticas, procedimientos operativos, o métodos sin necesidad de afectar al sistema real.
ALGUNAS DE LAS DEFINICIONES MAS ACEPTADAS
Simulación es una técnica numérica para conducir experimentos en una computadora digital. estos experimentos comprenden ciertos tipos de relaciones matemáticas y lógicas, las cuales son necesarias para describir el comportamiento y la estructura de sistemas complejos del mundo real a través de largos periodos de tiempo.
Thomas h. Naylor
Simulación es el desarrollo de un modelo lógico matemático de un sistema, de tal forma que se tiene una imitaciónde la operación de un proceso de lavida real o de un sistemaa través del tiempo. La simulación involucra la generación de una historia artificial de un sistema, la observación de esta historia mediante la manipulación experimental, nos ayuda a inferir las característicasoperacionales de tal sistema.
JERRY BANKS
Simulación es una técnica numérica para realizar experimentos en una computadora digital. estos experimentos involucran ciertos tipos de modelos matemáticos y lógicos que describen el comportamiento de sistemas de negocios, económicos, sociales, biológicos, físicos o químicos a través de largos periodos de tiempo.
H. MAISEL Y G. GNUGNOLI
Simulación es el proceso de diseñar y desarrollar un modelo de un sistema o proceso real y conducir experimentos con el propósito de entender el comportamiento del sistema o evaluar varias estrategias (dentro de límites impuestos por un criterio o conjunto de criterios) para la operación del sistema.
Robert. Shannon
Suscribirse a:
Comentarios (Atom)


